Exercice 1

Soit un vitrage simple d’épaisseur 5 mm, de coefficient de conductibilité λ = 1,15 W/m °C. La température de surface du vitrage intérieure est 22°C, la température de surface du vitrage extérieure 10°C.

1. Calculer la résistance thermique du vitrage
2. Déterminer le flux thermique dissipé à travers ce vitrage pour une surface de 10 m².

Exercice 2

La déperdition thermique d’un mur en béton de 30 m² de surface est 690 W.

Sachant que le mur a une épaisseur de 10 cm, et que la température de sa face intérieure est 25°C, calculer la température de la face extérieure.

On donne : λ béton = 1,75 W/m°C

Exercice 3

Soit un four constitué de trois épaisseurs différentes.

Mur 1 : brique réfractaire en silice e1 = 5 cm, λ1 = 0,8 W/(m.K)
Mur 2 : brique réfractaire en argile e2 = 5 cm, λ2 = 0,16 W/(m.K)
Mur 3 = brique rouge e3 = 5 cm, λ3 = 0,4 W/(m.K)

Température surface intérieure θ1 = 800°C
Température de surface extérieure θ2 = 20°C

1. Calculer la résistance thermique du four.
2. En déduire son coefficient global de transmission thermique.
3. Calculer le flux thermique pour 1 m²
4. Calculer les températures θ12 et θ23
5. Dessiner le mur à l’échelle et tracer l’évolution de température à l’intérieur de celui-ci

Exercice 4

Les murs latéraux d’un local industriel maintenu à la température constante θi = 20° C son réalisés en béton banché d’épaisseur e = 20 cm et de conductivité thermique, λ= 1,2 W.m-1.K-1

Les résistances thermiques superficielles interne et externe ont respectivement pour valeur :

1 / hsi = 0,11 W-1.m².K et l / hse = 0,06 W-1.m².K

1. Exprimer puis calculer la résistance thermique de la paroi.
2. Exprimer puis calculer la densité du flux thermique, φ, transmis lorsque la température extérieure est θ e = 0°C.
3. En déduire la quantité de chaleur transmise par unité de surface de la paroi et par jour.

Exercice 5

On se propose de comparer un simple vitrage, d’épaisseur 5 mm et un double vitrage constitué de deux vitres d’épaisseurs égales à 5 mm chacune séparées par une lame d’air de 1 cm d’épaisseur.

• La surface vitrée de l’appartement est de 15 m².
• Résistance de surface intérieure d’une vitre : rsi = 0,11 m² .K.W –1
• Résistance de surface extérieure d’une vitre : rse =  0,06 m² .K.W –1
• Résistance thermique d’une lame d’air de 1 cm : R = 0,14 m² .K.W-1
• Conductibilité du verre : λ = 1,15 W. m-1 .K-1
• Prix du kilowattheure : 0,11€. hors taxe – TVA : 18,60 % (sur le kwh)
• Température intérieure : 19°C.

1°) La température extérieure est de – 10°C.

1. Dans les deux cas (vitrage simple et vitrage double) calculer la puissance thermique perdue par toute la surface vitrée de l’appartement.
2. Quelle est la température de surface intérieure de ces deux vitrages ?

2°) On considérera que l’hiver dure 150 jours pendant lesquels la température extérieure moyenne est de +5°C.

1. Calculer l’énergie perdue dans chacun des deux cas.

b) En déduire l’économie réalisée en un hivers lorsqu’on remplace le simple vitrage par un double vitrage.

Exercice 6

Le mur d’un local est constitué de trois matériaux différents :

• Un béton d’épaisseur e1 = 15 cm à l’extérieur

(conductivité thermique λ1 = 0,23 W. m-1 .K-1).

• Un espace e2 = 5 cm entre les deux cloisons rempli de polystyrène expansé

(conductivité thermique λ2 = 0,035 W.m-1 .K-1).

• Des briques d’épaisseur e3 = 5 cm à l’intérieur

(conductivité thermique λ3 = 0,47 W. m-1 .K-1).

1°) On a mesuré en hiver, les températures des parois intérieures θi et extérieure θe qui étaient θi = 25°C et θe = -8°C.

a) Donner la relation littérale, puis calculer la résistance thermique du mur pour un mètre carré.

b) Donner la relation littérale, puis calculer le flux thermique dans le mur pour un mètre carré.

c) Calculer la quantité de chaleur transmise par jour à travers un mètre carré de mur, pour ces températures.

2°) Les résistances thermiques superficielles interne et externe du mur ont respectivement pour valeur :

1 / hi = 0,11 m² .K.W-1 et 1 / he = 0,06 m² .K.W-1.

a) A quels types de transfert thermique ces données se rapportent-elles ?

b) Calculer les températures ambiantes extérieures θae et intérieure θai.

Exercice 7

La paroi d’un four électrique industriel est constitué de plusieurs matériaux comme l’indique le schéma ci-dessous.

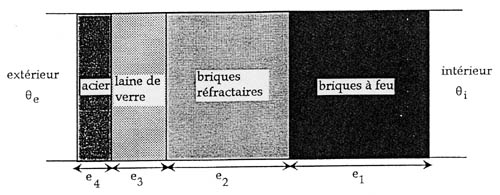
Données numérique :

Température ambiante intérieure : θi = 1092 °
Température ambiante extérieure : θe = 32°C
Surface intérieure du four : S = 8,00 m².
Résistance superficielle interne pour un m² de paroi : 1 / hi = ri = 0,036 m².K.W-1
Résistance superficielle externe pour un m² de paroi : 1 / he = re = 0,175m².K.W-1

Caractéristique des divers matériaux :

1. Exprimer littéralement puis calculer la résistance thermique globale R de un m² de paroi
2. Exprimer littéralement puis calculer la densité de flux thermique φ (puissance thermique par unité de surface) traversant la paroi.
3. Déterminer les températures au niveau des diverses interfaces : de l’intérieur vers l’extérieur θsi, θ1, θ2, θ3, θse.
4. Calculer le coût de fonctionnement journalier du jour sachant que le prix du Kw.h est 0,25€.

Exercice 8

1°) Citer les divers moles de transmission de la chaleur et donner dans chaque cas un exemple caractéristique.

2°) On note R la résistance thermique totale d’une paroi. Donner la relation existant entre la résistance thermique R, le flux thermique Φ à travers cette paroi, et l’écart de température ∆θ entre les deux faces de la paroi. Préciser l’unité de la résistance thermique R.

3°) On considère une maison assimilée à un parallélépipède rectangle de dimensions moyennes L, l , h. Les murs, en pierre mélangée à de la terre, ont une épaisseur moyenne e1 et une conductivité thermique λ1.

On suppose négligeable les pertes de chaleur par le sol, le plafond et les ouvertures. La valeur moyenne, sur la durée des quatre mois d’hiver, de la différence entre la température de la face intérieure et celle de la face extérieure du mur est notée ∆θ.

On donne :

e1 = 0,5 m
λ1 = 1,2 W m-1 K-1
L = 15 m
l = 10 m
H = 6 m
∆θ = 12° C.

1. Exprimer littéralement puis calculer la résistance thermique R de ces murs.
2. Exprimer littéralement puis calculer le flux thermique Φ transmis à travers l’ensemble des murs.
3. Le prix moyen du Kw.h est 0,14 €. Calculer le coût du fonctionnement d’un chauffage électrique permettant de compenser les pertes thermiques qui se produisent pendant les 120 jours de froid.

4°) Dans le cadre d’une réfection de la maison, on envisage de recouvrir les façades extérieures d’un enduit et de doubler intérieurement les murs par du placo-plâtre séparé du mur par du polystyrène.

On donne dans le tableau ci-dessous les épaisseurs e et les conductivités thermiques λ des divers matériaux.

1. Exprimer littéralement puis calculer la résistance thermique du mur isolé.
2. Calculer l’économie ainsi réalisée pendant les 120 jours de froid.

Created with the Personal Edition of HelpNDoc: Easy to use tool to create HTML Help files and Help web sites